key によるバッチ化

Test

---
skip_showdoc: true
---

N=10
T=1000 
G =  1/2**7 * jnp.identity(N, dtype=jnp.float32)
Sigma = 1.5 * jnp.identity(N, dtype=jnp.float32)
w0 = 0*jnp.ones((N,), dtype=jnp.float32)/jnp.sqrt(N)
P0 = G
propy1 = 0.5

batched_exper = jax.vmap(
  lambda key: Comp.RMS(key, N, T, G, w0, Sigma, P0, propy1)
)

master_key = jrd.PRNGKey(0)
keys = jrd.split(master_key, 1000)

W_norms, RMS_EKF, RMS_VA, RMS_EM = batched_exper(keys)

plt.scatter(W_norms.reshape(-1), RMS_EKF.reshape(-1))
plt.scatter(W_norms.reshape(-1), RMS_VA.reshape(-1), marker="x")
plt.scatter(W_norms.reshape(-1), RMS_EM.reshape(-1), marker=".")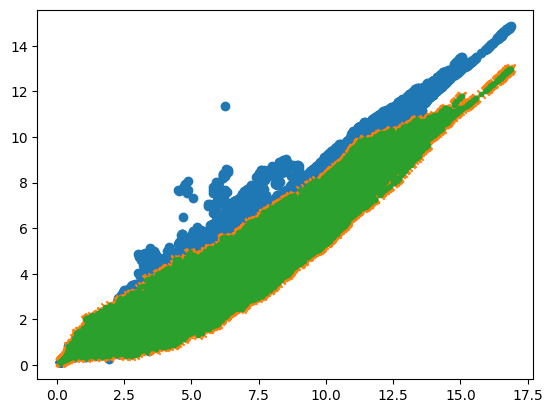

# bin の定義
bins = jnp.arange(0.1, 12, 0.1)
bin_edges = jnp.arange(0.0, 12.1, 0.1)  # 例: [0.0, 0.1, 0.2, ..., 12.0]

# 各要素が属するビンを計算 (1~len(bins) のインデックス)
bin_idx = jnp.digitize(W_norms.ravel(), bin_edges) - 1  # shape (T*N,)

# フラット化
ekf_flat = RMS_EKF.ravel()
va_flat  = RMS_VA.ravel()
em_flat = RMS_EM.ravel()

# 各 bin ごとの総和とカウントを計算
sum_ekf = jnp.bincount(bin_idx, weights=ekf_flat, length=len(bins))
sum_va  = jnp.bincount(bin_idx, weights=va_flat,  length=len(bins))
sum_em  = jnp.bincount(bin_idx, weights=em_flat,  length=len(bins))
counts  = jnp.bincount(bin_idx, length=len(bins))

# 平均を計算（ゼロ除算防止）
mean_ekf = jnp.where(counts > 0, sum_ekf / counts, jnp.nan)
mean_va  = jnp.where(counts > 0, sum_va / counts, jnp.nan)
mean_em  = jnp.where(counts > 0, sum_em / counts, jnp.nan)

# 最終結果をまとめる
df_source = jnp.stack([bins, mean_ekf, mean_va, mean_em], axis=1)

# Pandas DataFrame に変換（必要なら）
df = pd.DataFrame(jnp.array(df_source), columns=["bin", "EKF_RMS", "VA_RMS", "EM_RMS"]).set_index("bin")

df[0.8:10].head(20)

	EKF_RMS	VA_RMS	EM_RMS
bin
0.8	0.742320	0.743473	0.743350
0.9	0.839010	0.841791	0.841518
1.0	0.924905	0.927862	0.927469
1.1	1.016297	1.020453	1.019893
1.2	1.105977	1.110465	1.109501
1.3	1.174655	1.180493	1.179403
1.4	1.252368	1.259346	1.257725
1.5	1.327946	1.335311	1.333957
1.6	1.379003	1.375262	1.373536
1.7	1.458880	1.461715	1.460669
1.8	1.502239	1.492858	1.491333
1.9	1.553879	1.537835	1.536580
2.0	1.609895	1.585574	1.583595
2.1	1.650254	1.615584	1.614009
2.2	1.710323	1.670204	1.669090
2.3	1.770196	1.712925	1.711877
2.4	1.830160	1.768064	1.767073
2.5	1.889573	1.808915	1.808709
2.6	1.922787	1.830989	1.830768
2.7	1.968957	1.869247	1.869909

df[:2.7].plot()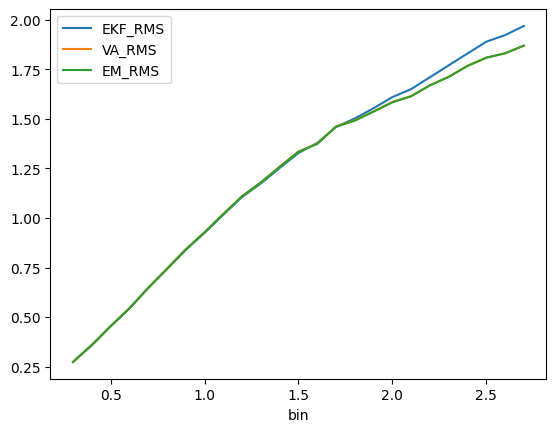

N=10
T=1000 
G =  1/2**9 * jnp.identity(N, dtype=jnp.float32)
Sigma = 0.5 * jnp.identity(N, dtype=jnp.float32)
w0 = 0*jnp.ones((N,), dtype=jnp.float32)/jnp.sqrt(N)
P0 = G
propy1 = 0.5

batched_exper = jax.vmap(
  lambda key: Comp.losi_error(key, N, T, G, w0, Sigma, P0, propy1)
)

master_key = jrd.PRNGKey(0)
keys = jrd.split(master_key, 1000)

RMS_EKF, RMS_VA, RMS_EM = batched_exper(keys)

RMS_EKF.sum(), RMS_VA.sum(), RMS_EM.sum()

(Array(1.0641768e+07, dtype=float32),
 Array(8.087362e+06, dtype=float32),
 Array(8.100394e+06, dtype=float32))

Ns = [2, 4, 8]
Gs = jnp.array([1/2**4, 1/2**6, 1/2**8, 1/2**10, 1/2**12])
Sigmas = jnp.array([1/2**2, 1/2, 1, 2, 4, 8])
propy1s = jnp.array([0.5, 0.1])

import pandas as pd

# 最初に空の DataFrame を用意
df = pd.DataFrame(columns=["N", "G", "Sigma", "propy1", "err_EKF_sc", "err_VA_sc", "err_EM_sc"])

for N in Ns:
  print("N", N)
  for G_ in Gs:
    print("G", G_)
    for Sigma_ in Sigmas:
      for propy1 in propy1s:
        T = 1000
        G = G_ * jnp.identity(N, dtype=jnp.float32)
        Sigma = Sigma_ * jnp.identity(N, dtype=jnp.float32)
        w0 = 0*jnp.ones((N,), dtype=jnp.float32)/jnp.sqrt(N)
        P0 = G
        batched_exper = jax.vmap(
          lambda key: Comp.losi_error(key, N, T, G, w0, Sigma, P0, propy1),
          in_axes=(0,)
        )
        master_key = jrd.PRNGKey(0)
        keys = jrd.split(master_key, 1000)

        err_EKF, err_VA, err_EM = batched_exper(keys)

        err_EKF_sc = jnp.sqrt(err_EKF.mean())
        err_VA_sc = jnp.sqrt(err_VA.mean())
        err_EM_sc = jnp.sqrt(err_EM.mean())

        # pandas df に追加
        df.loc[len(df)] = [
            int(N),
            float(G_),
            float(Sigma_),
            float(propy1),
            float(err_EKF_sc),
            float(err_VA_sc),
            float(err_EM_sc)
        ]

print(df.head())

N 2
G 0.0625
G 0.015625
G 0.00390625
G 0.0009765625
G 0.00024414062
N 4
G 0.0625
G 0.015625
G 0.00390625
G 0.0009765625
G 0.00024414062
N 8
G 0.0625
G 0.015625
G 0.00390625
G 0.0009765625
G 0.00024414062
     N       G  Sigma  propy1  err_EKF_sc  err_VA_sc  err_EM_sc
0  2.0  0.0625   0.25     0.5    0.092954   0.093325   0.093123
1  2.0  0.0625   0.25     0.1    0.092736   0.093197   0.092990
2  2.0  0.0625   0.50     0.5    0.093420   0.093336   0.093043
3  2.0  0.0625   0.50     0.1    0.093356   0.093240   0.092941
4  2.0  0.0625   1.00     0.5    0.093443   0.091697   0.091294

	N	G	Sigma	propy1	err_EKF_sc	err_VA_sc	err_EM_sc
2	2.0	0.062500	0.50	0.5	0.093420	0.093336	0.093043
4	2.0	0.062500	1.00	0.5	0.093443	0.091697	0.091294
6	2.0	0.062500	2.00	0.5	0.093836	0.089228	0.088805
8	2.0	0.062500	4.00	0.5	0.094327	0.086147	0.085870
10	2.0	0.062500	8.00	0.5	0.096139	0.082455	0.082723
18	2.0	0.015625	2.00	0.5	0.093420	0.093336	0.093043
20	2.0	0.015625	4.00	0.5	0.093443	0.091697	0.091294
22	2.0	0.015625	8.00	0.5	0.093836	0.089228	0.088805
34	2.0	0.003906	8.00	0.5	0.093420	0.093336	0.093043
48	2.0	0.000244	0.25	0.5	0.039164	0.039163	0.039163
60	4.0	0.062500	0.25	0.5	0.100617	0.099913	0.099700
62	4.0	0.062500	0.50	0.5	0.093656	0.091329	0.091214
64	4.0	0.062500	1.00	0.5	0.085952	0.080761	0.080898
66	4.0	0.062500	2.00	0.5	0.078222	0.070136	0.070658
68	4.0	0.062500	4.00	0.5	0.072354	0.060668	0.061745
70	4.0	0.062500	8.00	0.5	0.064038	0.051949	0.053414
76	4.0	0.015625	1.00	0.5	0.100617	0.099913	0.099700
78	4.0	0.015625	2.00	0.5	0.093656	0.091329	0.091214
80	4.0	0.015625	4.00	0.5	0.085952	0.080761	0.080898
82	4.0	0.015625	8.00	0.5	0.078222	0.070136	0.070658
92	4.0	0.003906	4.00	0.5	0.100617	0.099913	0.099700
94	4.0	0.003906	8.00	0.5	0.093656	0.091329	0.091214
120	8.0	0.062500	0.25	0.5	0.096732	0.091938	0.092006
122	8.0	0.062500	0.50	0.5	0.083484	0.076024	0.076319
124	8.0	0.062500	1.00	0.5	0.071028	0.062117	0.062546
126	8.0	0.062500	2.00	0.5	0.059638	0.050017	0.050485
128	8.0	0.062500	4.00	0.5	0.048867	0.039920	0.040344
130	8.0	0.062500	8.00	0.5	0.038852	0.031403	0.031772
132	8.0	0.015625	0.25	0.5	0.120174	0.119479	0.119283
134	8.0	0.015625	0.50	0.5	0.109672	0.107326	0.107210
136	8.0	0.015625	1.00	0.5	0.096732	0.091938	0.092006
138	8.0	0.015625	2.00	0.5	0.083484	0.076024	0.076319
140	8.0	0.015625	4.00	0.5	0.071028	0.062117	0.062546
142	8.0	0.015625	8.00	0.5	0.059638	0.050017	0.050485
146	8.0	0.003906	0.50	0.5	0.125066	0.124960	0.124792
148	8.0	0.003906	1.00	0.5	0.120174	0.119479	0.119283
150	8.0	0.003906	2.00	0.5	0.109672	0.107326	0.107210
152	8.0	0.003906	4.00	0.5	0.096732	0.091938	0.092006
154	8.0	0.003906	8.00	0.5	0.083484	0.076024	0.076319
156	8.0	0.000977	0.25	0.5	0.104002	0.103998	0.103986
162	8.0	0.000977	2.00	0.5	0.125066	0.124960	0.124792
164	8.0	0.000977	4.00	0.5	0.120174	0.119479	0.119283
166	8.0	0.000977	8.00	0.5	0.109672	0.107326	0.107210
168	8.0	0.000244	0.25	0.5	0.076621	0.076618	0.076616
170	8.0	0.000244	0.50	0.5	0.090635	0.090629	0.090625
172	8.0	0.000244	1.00	0.5	0.104002	0.103998	0.103986
178	8.0	0.000244	8.00	0.5	0.125066	0.124960	0.124792

df.groupby("propy1").mean()

	N	G	Sigma	err_EKF_sc	err_VA_sc	err_EM_sc
propy1
0.1	4.666667	0.01665	2.625	0.090087	0.087966	0.087953
0.5	4.666667	0.01665	2.625	0.090186	0.088121	0.088114

df1 = df[df["propy1"] == 0.5][["N", "G", "Sigma", "err_EKF_sc", "err_VA_sc", "err_EM_sc"]]

df1.shape

(90, 7)

損失関数と同じ評価関数

\[E=\|\hat{\mathbf w}_{t} - \mathbf w_t\|^2\]

新たに導入した評価関数: \[E=\sqrt{\frac{1}{T}\sum_t^T\left(\left[\sigma(\mathbf w_t^T\mathbf x_t) - \sigma(\hat{\mathbf w}_{t-1}^T\mathbf x_t)\right]^2\right)}\]

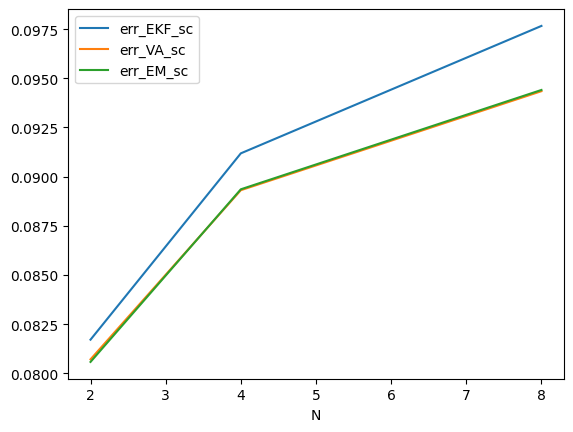
次元数 \(N\) に関しての比較

90 個のデータのうち、変分近似が拡張カルマンフィルタよりも \(E\) が大きかったデータは - \(N=2\) : 20/30 - \(N=4\) : 18/30 - \(N=8\) : 5/30

df1[(df1["err_EKF_sc"] < df1["err_VA_sc"])].groupby("N").count()

	G	Sigma	err_EKF_sc	err_VA_sc	err_EM_sc
N
2.0	20	20	20	20	20
4.0	18	18	18	18	18
8.0	5	5	5	5	5

遷移行列 \(\boldsymbol\Gamma=pI\) に関しての比較 90 個のデータのうち、変分近似が拡張カルマンフィルタよりも \(E\) が大きかったデータは [1/24, 1/26, 1/28, 1/210, 1/2**12] - \(p = 1/2^{12}\) : 13/18 - \(p = 1/2^{10}\) : 14/18 - \(p = 1/2^8\) : 10/18 - \(p = 1/2^6\) : 5/18 - \(p = 1/2^4\) : 1/18

df1[(df1["err_EKF_sc"] < df1["err_VA_sc"])].groupby("G").count()

	N	Sigma	err_EKF_sc	err_VA_sc	err_EM_sc
G
0.000244	13	13	13	13	13
0.000977	14	14	14	14	14
0.003906	10	10	10	10	10
0.015625	5	5	5	5	5
0.062500	1	1	1	1	1

\(\mathbf x_t\) の共分散行列 \(\Sigma=qI\) に関しての比較 [1/2**2, 1/2, 1, 2, 4, 8] - \(q = 1/2^2\) : 9/15 - \(q = 1/2\) : 9/15 - \(q = 1\) : 8/15 - \(q = 2\) : 7/15 - \(q = 4\) : 6/15 - \(q = 8\) : 4/15

df1[(df1["err_EKF_sc"] < df1["err_VA_sc"])].groupby("Sigma").count()

	N	G	err_EKF_sc	err_VA_sc	err_EM_sc
Sigma
0.25	9	9	9	9	9
0.50	9	9	9	9	9
1.00	8	8	8	8	8
2.00	7	7	7	7	7
4.00	6	6	6	6	6
8.00	4	4	4	4	4

df1[["G", "err_EKF_sc", "err_VA_sc", "err_EM_sc"]].groupby("G").mean().plot()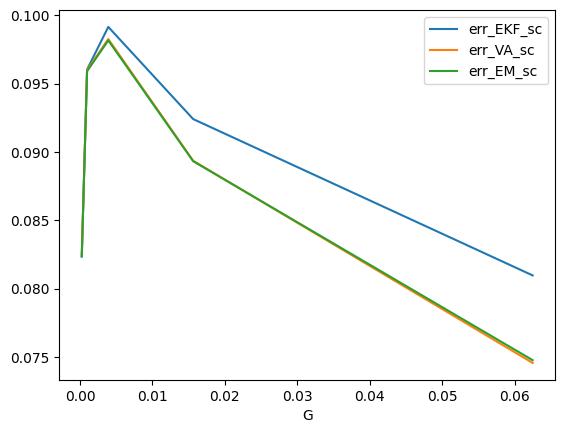

df1[["Sigma", "err_EKF_sc", "err_VA_sc", "err_EM_sc"]].groupby("Sigma").mean().plot()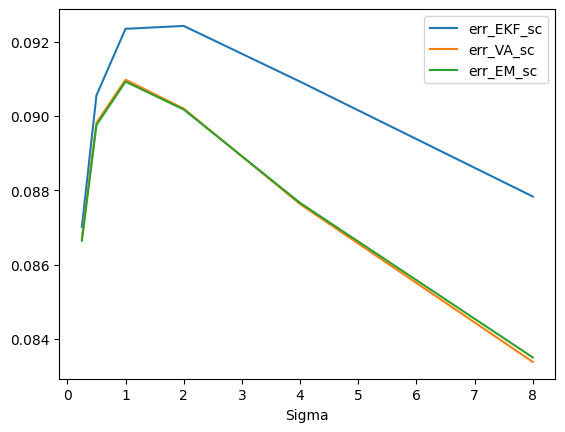

df1[["N", "err_EKF_sc", "err_VA_sc", "err_EM_sc"]].groupby("N").mean().plot()